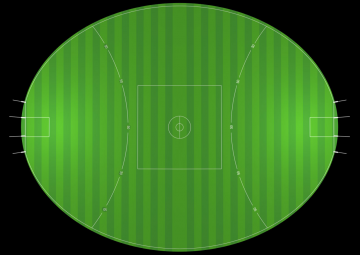
Marking Out the Playing Field

An oval is an ellipse:  the locus of points where the sum of the distances from any point on the curve to two fixed points is constant. The two fixed points are called foci.

You will want two pieces of rebar to hammer into the foci points and some string that can be pulled taught yet is not heavy string (you need to constantly be pulling the string straight as you walk around).  Pull the string tight (but you have to let it be sliding through your hand) as you walk around and have someone walk directly behind you with the painter.

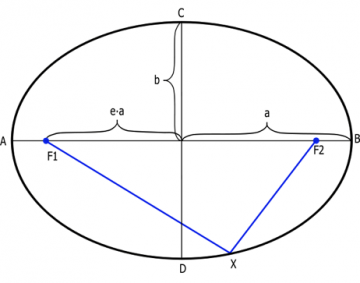
• Take note of the image on the following page which shows the distances A-B, C-D, a (which is half of A-B), and b (half of C-D), also note the distance (e-a).
• If you have unlimited room you can build a field to the dimensions of the MCG (A-B = 165 m, and C-D = 135 m).
• When you have limited space you can measure what you have available and calculate an ellipse for it.  Measure what you have (distance A-B and C-D).  Take off 5-10m for both axis to give some room for a boundary (and errors)
• Find the center of the ground and establish the major axis (tricky to do – you should just use best judgment and eyeball it) where the center of the goals will be.
• The distance (e-a) is the distance from the center of the ground to the foci points along the major axis.  This distance is calculated by the square root of the sum of (a2 – b2), note that a = A/2.  [example: for the ‘G, the distance (e-a) would be the square root of ((165/2)2 – (135/2)2) or (82.52 – 67.52)1/2 or (6806.25 – 4556.25)1/2 or 22501/2  or 47.43m ]
• The length of the string will be 2a (or the distance of the major axis, which is A-B)
• It would be beneficial to do it on a piece of foam board first using millimeters instead of meters.

An ellipse can be drawn with two pins, a loop of string, and a pencil.  The pins are placed at the foci and the pins and pencil are enclosed inside the string.  The pencil is placed on the paper inside the string, so the string is taut.  The string will form a triangle.  If the pencil is moved around so that the string stays taut, the sum of the distances from the pencil to the pins will remain constant, satisfying the definition of an ellipse.

The line segment AB, that passes through the foci and terminates on the ellipse, is called the major axis. The major axis is the longest segment that can be obtained by joining two points on the ellipse.  The line segment CD, which passes through the center (halfway between the foci), perpendicular to the major axis, and terminates on the ellipse, is called the minor axis.  The semi major axis (denoted by a in the figure) is one half the major axis: the line segment from the center, through a focus, and to the edge of the ellipse. Likewise, the semi minor axis (denoted by b in the figure) is one half the minor axis.

If the two foci coincide, then the ellipse is a circle; in other words, a circle is a special case of an ellipse, one where the eccentricity is zero.

Goal Square

Each goal square should measure 7 yards across the base and 9 yards in length, there should also be 7 yards between each behind and goal post (the end of the field is a straight line, so the oval is flat at each end, not curved.

Center Square

The center square should measure 50 meters on each side, however, you can decrease this to 45 meters should you be playing on a slightly smaller field.

In addition you need to mark 2 center circles. The first is to have a diameter of 3 meters (usually easiest to tie a piece of string around paint can of 1.5 meters in length, anchor to center point of field and draw circle).  Repeat for a larger circle, 5 meters length of twine to mark a 10 meter diameter circle.  The opposing ruckmen must start within this larger circle for center bouncedowns, and no other player can start within this circle.

50 Meter Arc

Additionally (Optional), you can mark the 50 meter arc.  Measure out a 50 meter length or rope, tie to paint tin, anchor on goal line halfway between goal posts, pull rope tight and mark arc.

Overhead View of Ground when Complete